Towards Tighter Convex Relaxation of Mixed-integer Programs: Leveraging Logic Network Flow for Task and Motion Planning

Xuan Lin1,2, Jiming Ren1,2*, Yandong Luo1,2*, Weijun Xie3, Ye Zhao1,2,
1George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA, 2Institute for Robotics and Intelligent Machines (IRIM), Georgia Institute of Technology, USA 3Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, USA
Paper arXiv Video Code

TL;DR: Logic Network Flow (LNF) is a novel formulation for temporal logic specifications with provably tighter convex relaxations and fewer constraints than standard Logic Tree approaches, achieved by projecting Graph-of-Convex-Sets onto lower-dimensional spaces using Fourier-Motzkin elimination.

fig_Fourier image

Abstract

This paper proposes an optimization-based task and motion planning framework, named "Logic Network Flow" (LNF), to integrate temporal logic specifications into efficient mixed-integer programs. Temporal predicates are encoded as polyhedron constraints on each edge of a network flow model, instead of as constraints between nodes as in traditional Logic Tree formulations. This leads to provably tighter convex relaxations and fewer constraints when synthesized with various piecewise-affine (PWA) dynamic system formulations. Comprehensive experiments across vehicle routing, multi-robot coordination, and temporal logic control on dynamical systems using point mass and linear inverted pendulum models demonstrate up to orders of magnitude computational speedups.

Paper Video

Experiments

Multi-robot Path Planning for Search and Rescue Application

Three bipedal robots coordinate to execute search and rescue operations, equipment retrieval, and fire extinguishing tasks in a disaster zone.

Bipedal Locomotion TAMP with Linear Inverted Pendulum Dynamics and Safe Footstep Regions

Optimized footstep planning for bipedal walking robots using temporal logic specifications with safe contact regions.

Temporal Path Planning for Multi-Agent Systems

Three robots follow conflict-free trajectories to complete tasks across multiple rooms, demonstrating efficient path planning and scheduling.

Dynamic Replanning under Temporal Logic Constraints

A quadruped robot is physically dragged off course and encounters a new obstacle. It dynamically replans under temporal logic to reach an alternative feasible target.

Computational Performance: Vehicle Routing with Temporal Logic

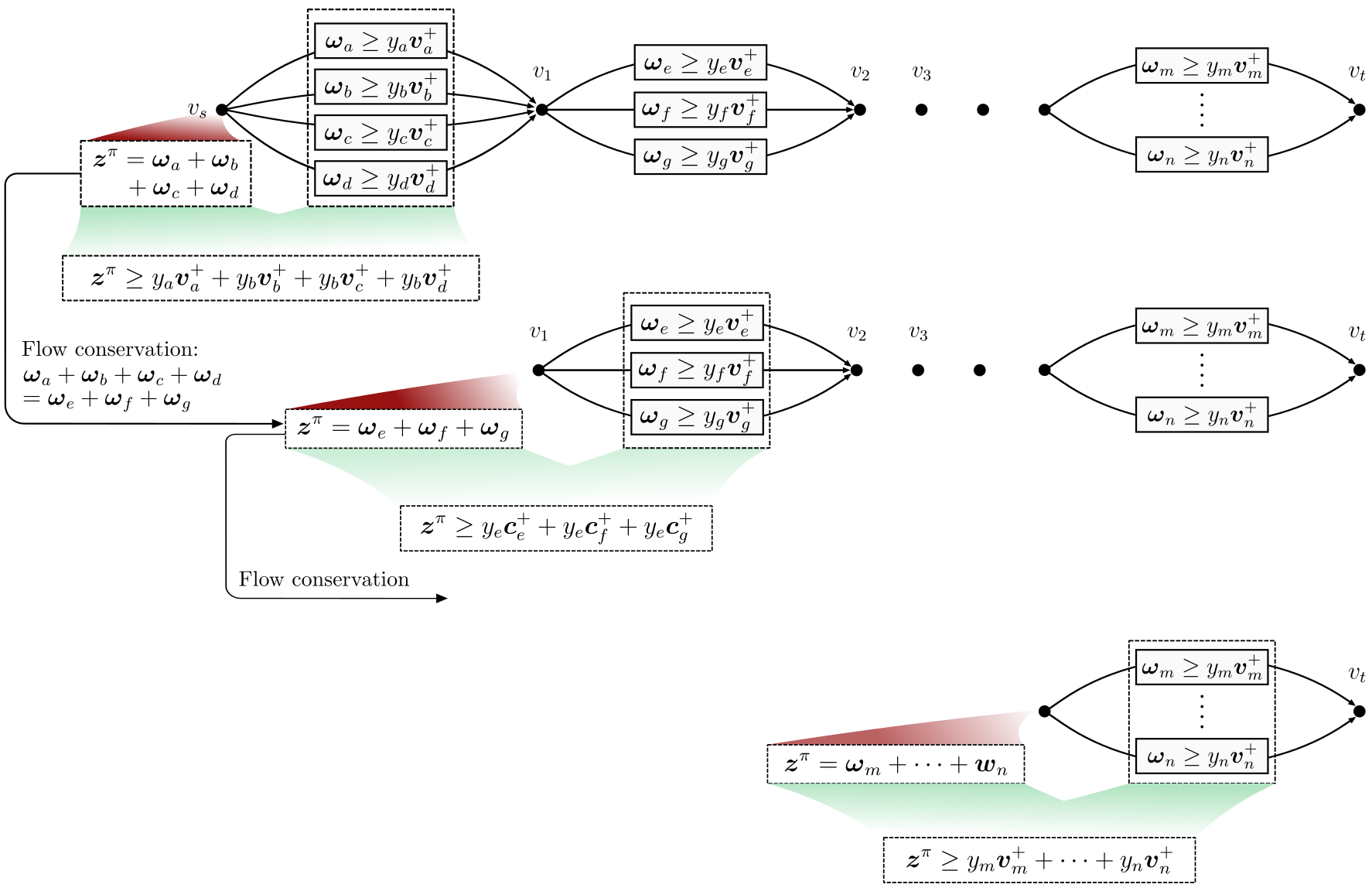
For vehicle routing problems formulated as temporal logic specifications with dynamic network flow, our computational results demonstrate that LNF achieves consistently tighter convex relaxation gaps, leading to significant speedups compared to Logic Tree formulations across different problem sizes.

Table: Computation results for vehicle routing with temporal logic specifications (50 trials, 10,000s timeout)
3 Robots, 9 Tasks, N=50 6 Robots, 18 Tasks, N=70
LNF LNF-w/o F-M LT Speedup LNF LNF-w/o F-M LT Speedup
# binary vars 245 245 245 - 1242 1242 1242 -
# continuous vars 17,645 242,800 17,656 - 48,994 1,524,490 49,013 -
# constraints 9,614 241,264 11,897 - 26,376 1,527,738 32,283 -
Root relaxation gap (%) 6.7±3.1 6.7±3.1 31.2±4.3 - 8.1±2.0 8.1±2.0 38.0±1.7 -
Gurobi T-Find (10%) 1.1±0.4 266.0±89.5 5.7±2.3 5× 49.2±5.3 2580.9±1161.4 1178.8±244.9 24×
T-Find (optimal) 1.8±0.6 643.8±329.1 22.6±14.9 12× 570.0±245.9 Timeout Timeout >18×
T-Prove (10%) 1.2±0.4 337.7±117.3 22.4±14.5 19× 49.4±6.5 3675.0±893.3 1990.6±810.0 40×
T-Prove (optimal) 1.7±0.8 1202.6±849.9 52.9±34.6 31× 779.2±409.8 Timeout Timeout >13×
CPLEX T-Prove (optimal) 13.0±9.6 Timeout 4475.7±3501.7 344× 1127.0±566.0 Timeout Timeout >9×

Acknowledgments

This work was supported by the Office of Naval Research (ONR) under Grant N000142312223.

BibTeX

@article{}